ABN algoritmoa, gure ohiko algoritmoa: batuketak

Bagoaz  batuketak egiteko 11 moduetatik bi aztertzera. Elkarren segidan garatuko ditugu alderatu ahal izateko.

Jo dezagun 26 lagun goazela ibilaldi batera gure herritik eta beste 19k eman dutela izena alboko herrian.  Zenbat lagun elkartuko gara autobusean?

Gure ohiko algoritmoaz honela egingo genuke: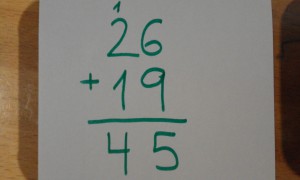

Gurea, ohikoa:

• Zenbakia osatzen duten zifratan oinarritzen da. Hau da, metodo honekin egiten den batuketa haundiena 9+9 da
• Instrukzio zehatzak bete behar dira egin ahal izateko. Bateko eta hamarrekoan lerrokatuta jarri bertikalean; batekoetatik hasi; 10 baino gutxiago ematen badu lasai eta hamar baino gehiago ematen badu bateko txiki bat gehitu hurregoa zutabeari eta azkenik ekin azken zutabea batzeari. Orain bai, hamar baino gehiago ematen badu edo ez badu, zenbaki osoa idazten da behean.
• Modu bakarra dago batuketa egiteko.
• Emaitza nondik norakoa izango den ez da bukaerarate jakiten.

ABN metodoarekin honela egingo litzateke eragiketa:

 Ikus dezagun zer esaten ari zaigun taula hau: ABN sisteman, zenbaki baten gainera batzen da beste zenbakia poliki-poliki. Gura adibidean, 26+19 egitera goazenez aukeratu egiten dut 26ren gainera batzea 19. Aukera hori egin eta gero zera erabakitzen dut:

1. pausuan: 4 gehituko dizkiot 26ri eta horrela 30era iristen naiz. Oraindik 15 geratzen zaizkit batzeko.
2. pausuan: Orain beste 10 gehituko dizkiot eta horrela 40ra iirsten naiz. Oraindik 5 geraten zaizkit batzeko.
3. pausuan: azken 5ak gehitzen ditut eta horrela bukatu dut eragiketa; autobusean 45 lagun elkartuko garela diosku emaitzak.

Hemen ikusi dugun bezala egin behar da nahitaez? Ez; bakoitzak aukeratzen du zein zenbaki zeini batu eta batez ere zenbat pausuatan egin. Ikus ditzagu eragiketa berbera egiteko beste bi modu.  

26ri gehitu diogu 19 berriz ere baina lehenego pausuan 10 gehitzea erabaki dugu; gero beste 4 eta gero beste 5.

Orain 19 hartu dugu oinarri moduan eta 26 gehitu dikiot 4 pausutan. Gutxiagotan ere egin nezakeen nahi izan banu.

……..

“Ez da ba gauza haundia” pentsatu nuen nik hau lehenengo aldiz ikusi nuenean. “Are gehiago, nik neuk horrela egiten ditut kalkuluak buruz ari naizenean”, hori ere pentsatu nuen. Zuei ere gertatu al zaizue?

Kontua da begiratu sakonago bat egiten badiogu, honelako ezaugarriak ikusiko dizkiogula sistema honi:

• Zifratan baino, zenbakietan oinarritzen da. “Algoritmo Basado en Números” esan nahi baitu ABNk. Hau da, zenbaki osoak mobilizatzen dira eta ez zenbakien zifrak.
• Edozien tokitatik eta edozein pausurekin hasi daiteke. Ez dago batekotatik hasi beharrik, zutabean jarrita… Norberari ziurtasuna ematen dion lehenengo pausua aukeratzen da.
• Batuketa bera egiteko moduak anitzak dira. “Infinito” esango luke nire seme ertainak! Egin daiteke 2 pausutan edo 7 pausutan edo banan- banan batuta. 
• Ez dago hamarreko edo “llebadaren” beharrik. Berdin-berdinak dira hamarreko gabeko eta hamrrekodun batuketak; ez dira bereizten.
• Ariketak aurrera egin ahala eta zenbakietan gora egin ahala somatzen da emaitza gutxi gorabehera zein zenbakiren inguruan egongo den.
• Eragiketaren edozein momentutan galdetu eta erantzun daiteke hasieran planteatu dugun egoeraren inguruko azpi-galdera bat; adibidez, esan daiteke alboko herrian 4 apuntatu balira, 30 joango ginatekela autobusean;

 Sistema honetan oso inportanteak dira zenbaki zerrendako “mugarriak”. Izan ere, askotan aukeratzen dugu ahal bada hamarreko betea den toki batera iristea. Hau da, lehenengo pausuan 26ri 4 baten dizkiodanean, 30era iristeak lasaitzen nauelako da. Hortik beste 10 batzea oso erraza egiten zaidalako. Horregatik, metodoa aplikatzen den lekuetan asko lantzen dituzte “los amigos del 10” kontzpetua edo 10en deskonposaketa; 1eta 9, 2 eta 8, 3 etat 7… eta asko lantzen dituzte baita ere eragiketen anpliazioak:  26+4 30 bada,  46+4=50 dela eta 76+4=80 dela, alegia. Beste ezaugarri bat, gelan txotxekin 10eko paketeak eginaz jarduten dutela da, materialekin. alegia, eta beti, egoera bat ebazteko; beti asmatzen dituzte egoerak eragiketak burutzeko. 

Zergatik dut hain gustuko batuketak egiteko modu hau?

• Egokitu egiten delako bakoitzaren trebezietara. Kalkuluan trebea denak pausu pare baten eginda eukiko du eta polikiago ari denak pausu gehiago egin beharko ditu.
• Ez dago apenas instrukzio mekaniko eta itsurik.
• Igeri egiten da zenbakien katean barrena; eragiketa bakoitza da aberasgarria, kalkulurako gaitasunak  garatzen jarraitzen baita pausu bakoitzean. Efektu biderkatzailea daukala esaten dut nik. 
• Hamarrekoen gaia tartetik kentzen du (kenketekin ere bai!). Zenbaki haundiekin eragiketak egiten hasteko ez dago teknika garatzeari itxaron beharrik. Berehala hasi daiteke batuketa haundiagoak egiten. 
• Eragiketak autobuseko partaide kopuruarekin daukan lotura, hasierako egoerarekin alegia,  pausu guztietan mantentzen du. Ez da erlazioa eteten; ez dago azken pausuari itxaron beharrik zentzuzko zerbait topatzeko.

etodo honekin jardutea erabaki dutenek diotenez -nik ez baititut esperientziak bertatik bertara ezagutu- emaitzak inpresionanteak dira. Bai kalkulu gaitasunetan eta baita ere egoerak edo buruketei aurre egiteko gaitasunetan.

Ikus ezazue benetako adibide bat bideo honetan. LHko 1. mailakoa da mutiko hau.

Zeri iruditu zaizue? Gustura ikusiko nituzke zuen komentarioak!

Partekatu

Email

Facebook

0

Twitter

Pinterest

0

Whatsapp